CUADRICAS

SUMARIO

1. Definición

2. El elipsoide

3. Hiperboloide de una hoja

4. Hiperboloide de dos hojas

5. Cono elíptico

6. Paraboloide elíptico

7. Paraboloide hiperbólico

8. Cilindros
8.1. Cilindro elíptico:
8.2. Cilindro hiperbólico:
8.3. Cilindro parabólico:

9. Superficies cuádricas de revolución
9.1. Elipsoide de revolución
9.2. Hiperboloide de revolución
9.3. Paraboloide de revolución

Definición
Se denominan superficies cuádricas a todas aquellas superficies que pueden ser definidas mediante una ecuación de segundo orden.
Estas figuras responden a la siguiente expresión cuadrática general:

A continuación se exponen las citadas superficies acompañadas de sus respectivas ecuaciones referidas a su sistema de ejes:

El elipsoide
Un elipsoide es la superficie engendrada por una elipse de semiejes variables a y b que se mueve perpendicularmente al eje 2c de una segunda elipse, de forma que los extremos del eje 2a se apoyan continuamente sobre la segunda elipse, y el eje 2b varía según una relación de semejanza establecida respecto del eje 2a.

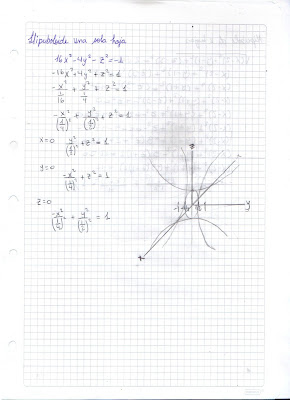
Hiperboloide de una hoja
Es el cuerpo engendrado por una elipse que se mueve de forma paralela y semejante a sí misma, apoyando continuamente los extremos de sus ejes sobre las dos ramas de una hipérbola.



Hiperboloide de dos hojas
Si la elipse del cuerpo anterior se apoya únicamente en la parte interior de una rama de la hipérbola y posteriormente en la otra, entonces resulta el hiperboloide de dos hojas.

Cono elíptico
Un cono elíptico es el cuerpo engendrado por una recta que, pasando continuamente por un punto O, se apoya sobre dos elipses paralelas e iguales situadas simétricamente respecto de un plano que contiene al punto citado.
El cono, por consiguiente, está constituido por dos superficies iguales dispuestas de forma especular respecto de un plano que pasa por el punto O (vértice del cono).

Paraboloide elíptico
El paraboloide, análogamente a la parábola en las secciones cónicas, es una superficie sin centro que, en el caso general de ser elíptico, se define como:
Aquella superficie que engendra una elipse variable al moverse de forma perpendicular sobre el eje de una parábola, de forma que mantiene constantemente los vértices de uno de sus ejes sobre dicha curva.

Paraboloide hiperbólico
Es la superficie engendrada por una hipérbola que, conservándose semejante a sí misma, se mueve a lo largo de una parábola directora. También puede definirse como la superficie generada por una parábola que, conservándose semejante a sí misma, se mueve a lo largo de una de las ramas de una hipérbola directora.

Cilindros
La ecuación general de las cuádricas puede representar también superficies cilíndricas, cuyas secciones correspondientes son curvas de segundo orden denominadas directrices del cilindro.
Según sea la curva directriz, el cilindro puede ser elíptico, hiperbólico o parabólico, definiéndose respectivamente como:
La superficie engendrada por una elipse, hipérbola o parábola que se mueve paralelamente a sí misma, manteniendo su centro o vértice sobre una recta perpendicular a su plano.
– Cilindro elíptico:

– Cilindro hiperbólico:

– Cilindro parabólico:

Superficies cuádricas de revolución
Las superficies vistas en los apartados anteriores adquieren especial importancia cuando resultan engendradas por rotación de una curva alrededor de un eje. En estos casos las ecuaciones reducidas se simplifican notablemente al ser iguales al menos dos de los parámetros que en ellas intervienen. Como tales, estas superficies se caracterizan por la existencia de un plano sobre el cual la sección producida por la figura es una circunferencia.
Dejando aparte los cilindros y conos de sección circular, destacamos las siguientes:
*Elipsoide de revolución. Es la superficie engendrada por la rotación de una elipse alrededor de uno de sus ejes. En consecuencia, la ecuación reducida de esta figura podría ser, por ejemplo:

*Hiperboloide de revolución. Es la superficie engendrada por rotación de una hipérbola alrededor de uno de sus ejes. Si el eje en cuestión es el eje imaginario, el hiperboloide será de una hoja, y si la rotación se produce en torno al eje focal o real, se obtiene el hiperboloide de dos hojas.
*Paraboloide de revolución. Es la superficie engendrada por la rotación de una parábola alrededor de su propio eje.

Ejemplos aplicables a la realidad en los negocios o la economía
Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley de gravitación universal, sus trayectorias describen secciones cónicas si su centro de masa se considera en reposo. Si están relativamente próximas describirán elipses, si se alejan demasiado describirán hipérbolas o parábolas.

También son importantes en aerodinámica y en su aplicación industrial, ya que permiten ser repetidas por medios mecánicos con gran exactitud, logrando superficies, formas y curvas perfectas.

Elipse es la curva que aparece con más frecuencia en la vida cotidiana.
La trayectoria de un objeto móvil que describe una orbita cerrada bajo la anuencia de una fuerza central inversamente proporcional al cuadrado de la distancia.

Las hipérbolas aparecen en algunas aplicaciones aeronáuticas. Supongamos que un avión vuela a una altura h sobre la superficie terrestre a la velocidad supersónica v. Se plantea el problema de determinar la región de la superficie terrestre en cuyos puntos y en un momento determinado se oye o se ha oído el sonido del motor del avión.

La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.

Se utilizan técnicas circunferenciales para muchas cosas. Por ejemplo; Los Cds,
La Circunferencia en el Transporte
En el transporte también podemos apreciar la presencia de la Circunferencia, de hecho, donde se puede notar y ejemplificar mejor es en la Bicicleta, un conjunto de tubos metálicos con dos ruedas que aplican la geometría perfectamente: Las ruedas están hechas de un “arco”
La Circunferencia, también presente en la Naturaleza:
La circunferencia también está presente en la naturaleza, aunque no sea totalmente precisa.
Los árboles, tipos de vida antiquísimos, crecen con el pasar de los años. Primero crecen pequeñas ramificaciones desde el suelo. Luego crecen más y con esto va aumentando el grosor de su Tronco.


EJERCICIOS